Chapter 1 B-27
Copyright © Houghton Mifflin Company. All rights reserved.
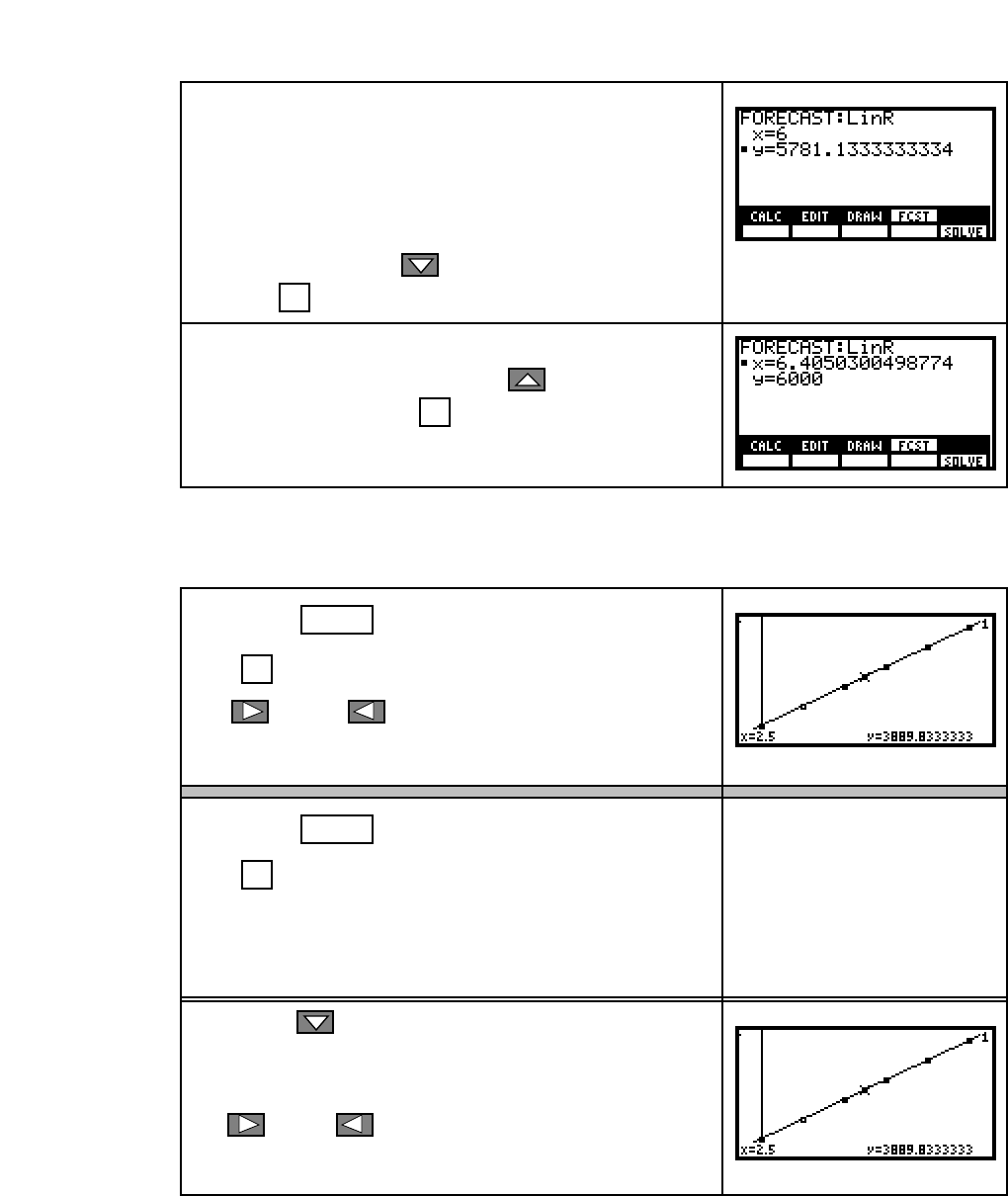
Predict the tax owed in 1998 where the tax is found
using the linear model computed from the data given
in Section 1.4.1 of this Guide:
Tax = 540.37143t + 2538.90476 dollars and t is the
number of years since 1992.
Note that 1998 is six years since 1992, so x = 6. Enter 6
in the x location, press to move to the y location,
and press F5 (SOLVE) .
The 1998 tax is predicted to
be about $5781.
Predict the year in which the tax will be $6000.
Enter 6000 in the y location, press to move to
the x location, and press F5 (SOLVE) . Remember
the data is aligned, so the answer is about 1992 + 6.4
or near the middle of 1999.
1.4.11 COPYING GRAPHS TO PAPER Your instructor may ask you to copy what is on your
graphics screen to paper. If so, use the following to more accurately perform this task.
TI-85 Press GRAPH to return the graph to the screen.
Press F4 (TRACE) to trace the graph.
Use and/or to locate several values that
are as ÒniceÓ as possible and mark those points on your
paper. Use a ruler to connect the linear model points.
TI-86 Press GRAPH to return the graph to the screen.
Press F4 (TRACE) to trace the graph. The P1 in the
upper right-hand corner of the screen indicates that
you are tracing the scatter plot of the data. Use either
these trace values or the data lists to mark the data
points on your paper.
Both Press to move the trace cursor to the linear
model graph. The number 1 at the top right of the
screen tells you which function you are tracing (in this
case, y1 ).
Use and/or to locate values that are as ÒniceÓ
as possible and mark those points on your paper. Use a
ruler to connect the model points and draw the line.
1.4.12 WHAT IS ÒBEST FITÓ? Even though your calculator easily computes the values
a
and
b for the best fitting linear model
y = ax + b, it is important to understand the method of
least-squares and the conditions necessary for its application if you intend to use this model.
You can explore the process of finding the line of best fit with program LSLINE. (Program
LSLINE is given in the TI-85/TI-86 Appendix.) For your investigations of the least-squares
