Chapter 1 B-17
Copyright © Houghton Mifflin Company. All rights reserved.
On the TI-85,
¥ The TI-85 interprets y1(y2) as the product of y1 and y2. To have the calculator graph the
composite function f(g(x)), you should substitute g(x) everywhere an x appears in f(x).
For instance, if f(x) = x
2
- 1 is in y1 and g(x) = 0.3x + 5 is in y2, enter y7 = y2
2
Ð 1 for the
composite function (f
o
g)(x) .
On the TI-86,
¥ Enter y1(y2 ) in y7 to obtain the composite function (f
o
g)(x) = f(g(x)).
Both Your calculator will evaluate and graph these constructed functions. Although it will
not give you an algebraic formula for a constructed function, you can check your algebra by
evaluating the calculator-constructed function and your constructed function at several
different points. (You will very likely have to reset the horizontal and vertical views when
graphing constructed functions.)
1.3.1 GRAPHING PIECEWISE CONTINUOUS FUNCTIONS Piecewise continuous
functions are used throughout the text. It is often helpful to use your calculator to graph and
evaluate outputs of piecewise continuous functions. Consider the following example.
The population of West Virginia from 1985 through 1993 can be modeled by
Pt
tt
tt
()
..
..
=
+£<
+££
ì
í
î
-
23 514 3903 667 85 90
9 1 972 6 90 93
thousand people when
thousand people when
where t is the number of years since 1900.
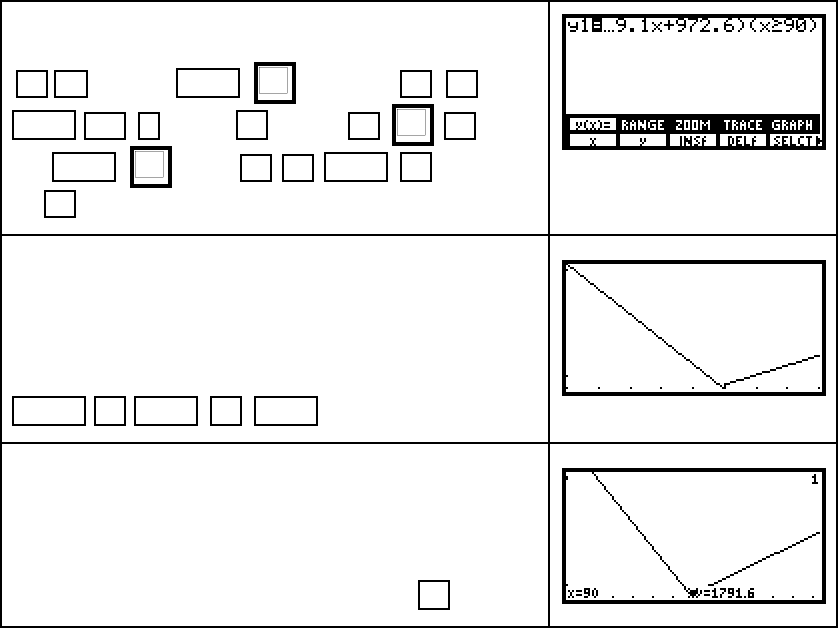
Enter the function P(t), using x as the input variable,
in the y
1 location of the y(x)= list using the keystrokes
(–)
23.514 x-VAR
+
3903.667
x-VAR 2nd 2 (TEST) F2 (<) 90
+
9.1 x-VAR
+
972.6
x-VAR F5 (³)
90
.
Each piece of the function and
its corresponding input must
be enclosed in parentheses.
Notice that the function is defined only when the input
is between 85 and 93. You could find P(85) and P(93) to
help you set the vertical view. However, we choose to
let the calculator set the vertical view.
Set the horizontal view xMin = 85 and xMax = 93. Press
GRAPH F3 MORE F1 ZOOM (ZFIT) to graph P(x).
If you wish to see the ÒbreakÓ in the function where
the two pieces join, the width of the screen must be a
multiple of 12.6 and include 90.
Since 90 Ð 0.5(12.6) = 83.7 and 90 + 0.5(12.6) = 96.3,
change xMin and xMax to these values. Press F5 (GRAPH) .
